WuTao's Blog

比赛链接：2016 ICPC Mid-Central USA Region
题目链接：Windy Path

Description

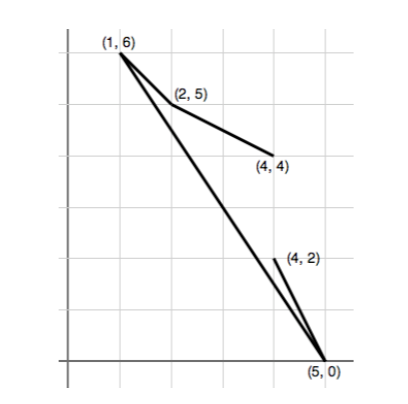
Consider following along the path in the figure above, starting from $(4,4)$ and moving to $(2,5)$. Then the path turns rightward toward $(1,6)$, then sharp left to $(5,0)$ and finally sharp left again to $(4,2)$. If we use ‘$L$’ for left and ‘RR’ for right, we see that the sequence of turn directions is given by RLL. Notice that the path does not cross itself: the only intersections of segments are the connection points along the path.

Consider the reverse problem: Given points in an arbitrary order,say $(2,5),(1,6),(4,4),(5,0),(4,2)$,could you find an ordering of the points so the turn directions along the path are given by RLL? Of course to follow the path in the figure,you would start with the third point in the list $(4,4)$,then the first $(2,5)$,second $(1,6)$, fourth $(5,0)$, and fifth $(4,2)$, so the permutation of the points relative to the given initial order would be: $3 1 2 4 5$.

题目链接：POJ 3468

Description

You have $N$ integers, $A_1, A_2, … , A_N$. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

2019 杭电多校 7 1006

题目链接：HDU 6651

比赛链接：2019 Multi-University Training Contest 7

Problem Description

Final Exam is coming! Cuber QQ has now one night to prepare for tomorrow’s exam.

The exam will be a exam of problems sharing altogether $m$ points. Cuber QQ doesn’t know about the exact distribution. Of course, different problems might have different points; in some extreme cases, some problems might worth $0$ points, or all $m$ points. Points must be integers; a problem cannot have $0.5$ point.

What he knows, is that, these $n$ problems will be about $n$ totally different topics. For example, one could be testing your understanding of Dynamic Programming, another might be about history of China in 19th century. So he has to divide your night to prepare each of these topics separately. Also, if one problem is worth $x$ points in tomorrow’s exam, it takes at least $x+1$ hours to prepare everything you need for examination. If he spends less than $x+1$ hours preparing, he shall fail at this problem.

Cuber QQ’s goal, strangely, is not to take as much points as possible, but to solve at least $k$ problems no matter how the examination paper looks like, to get away from his parents’ scoldings. So he wonders how many hours at least he needs to achieve this goal.

题目链接：Watch Where You Step

题意

给定有向图的邻接矩阵，现在需要给该图增加边，使得如果两点可达必直接可达，求需要加边的数量。

题目链接：Coins

Description

Alice and Bob are playing a simple game. They line up a row of nn identical coins, all with the heads facing down onto the table and the tails upward.

For exactly mm times they select any kk of the coins and toss them into the air, replacing each of them either heads-up or heads-down with the same possibility. Their purpose is to gain as many coins heads-up as they can.

题目链接：HDU 1548

Description

There is a strange lift.The lift can stop can at every floor as you want, and there is a number Ki(0 <= Ki <= N) on every floor.The lift have just two buttons: up and down.When you at floor i,if you press the button “UP” , you will go up Ki floor,i.e,you will go to the i+Ki th floor,as the same, if you press the button “DOWN” , you will go down Ki floor,i.e,you will go to the i-Ki th floor. Of course, the lift can’t go up high than N,and can’t go down lower than 1. For example, there is a buliding with 5 floors, and k1 = 3, k2 = 3,k3 = 1,k4 = 2, k5 = 5.Begining from the 1 st floor,you can press the button “UP”, and you’ll go up to the 4 th floor,and if you press the button “DOWN”, the lift can’t do it, because it can’t go down to the -2 th floor,as you know ,the -2 th floor isn’t exist.

Here comes the problem: when you are on floor A,and you want to go to floor B,how many times at least he has to press the button “UP” or “DOWN”?

题目链接：HDU 2266

Description

Now give you an string which only contains 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9.You are asked to add the sign ‘+’ or ’-’ between the characters. Just like give you a string “12345”, you can work out a string “123+4-5”. Now give you an integer N, please tell me how many ways can you find to make the result of the string equal to N .You can only choose at most one sign between two adjacent characters.

题目链接：POJ 3641

Description

Fermat’s theorem states that for any prime number p and for any integer a > 1, ap = a (mod p). That is, if we raise a to the pth power and divide by p, the remainder is a. Some (but not very many) non-prime values of p, known as base-a pseudoprimes, have this property for some a. (And some, known as Carmichael Numbers, are base-a pseudoprimes for all a.)

Given 2 < p ≤ 1000000000 and 1 < a < p, determine whether or not p is a base-a pseudoprime.

题目链接：POJ 1995

Description

People are different. Some secretly read magazines full of interesting girls’ pictures, others create an A-bomb in their cellar, others like using Windows, and some like difficult mathematical games. Latest marketing research shows, that this market segment was so far underestimated and that there is lack of such games. This kind of game was thus included into the KOKODáKH. The rules follow:

Each player chooses two numbers Ai and Bi and writes them on a slip of paper. Others cannot see the numbers. In a given moment all players show their numbers to the others. The goal is to determine the sum of all expressions AiBi from all players including oneself and determine the remainder after division by a given number M. The winner is the one who first determines the correct result. According to the players’ experience it is possible to increase the difficulty by choosing higher numbers.

You should write a program that calculates the result and is able to find out who won the game.