LightOJ 1418 Trees on My Island (Pick定理)

Problem Description

I have bought an island where I want to plant trees in rows and columns. So, the trees will form a rectangular grid and each of them can be thought of having integer coordinates by taking a suitable grid point as the origin.

But, the problem is that the island itself is not rectangular. So, I have identified a simple polygonal area inside the island with vertices on the grid points and have decided to plant trees on grid points lying strictly inside the polygon.

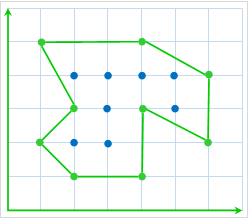
Figure: A sample of my island

For example, in the above figure, the green circles form the polygon, and the blue circles show the position of the trees.

Now, I seek your help for calculating the number of trees that can be planted on my island.

Input

Input starts with an integer $T (≤ 100)$, denoting the number of test cases.

Each case starts with a line containing an integer $N (3 ≤ N ≤ 10000)$ denoting the number of vertices of the polygon.

Each of the next $N$ lines contains two integers $x_i y_i (-10^6 ≤ x_i, y_i ≤ 10^6)$ denoting the co-ordinate of a vertex. The vertices will be given in clockwise or anti-clockwise order. And they will form a simple polygon.

Output

For each case, print the case number and the total number of trees that can be planted inside the polygon.

Sample Input

Sample Output

Case 1: 8

Note

Dataset is huge, use faster I/O methods.

Solution

题意：

给定一个多边形，顶点都在格点上，求多边形内部的格点个数。

思路

Pick 定理裸题。

#include <cstdio>
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;  
const db pi = acos(-1.0);  
const ll inf = 0x3f3f3f3f3f3f3f3f;  
const ll maxn = 1e5 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    ll x, y;
    Point(ll x = 0, ll y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lld%lld", &x, &y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    ll cross(const Point a) {
        return x * a.y - y * a.x;
    }
};

Point p[maxn];

ll gcd(ll a, ll b) {
    return b == 0? a: gcd(b, a % b);
}

int main() {
    int T;
    scanf("%d", &T);
    for(int _ = 1; _ <= T; ++_) {
        int n;
        scanf("%d", &n);
        ll on = 0;
        ll s = 0;
        for(int i = 0; i < n; ++i) {
            p[i].input();
        }
        p[n] = p[0];
        for(int i = 0; i < n; ++i) {
            s += (p[i + 1] - p[0]).cross(p[i] - p[0]);
            on += gcd(abs(p[i].x - p[i + 1].x), abs(p[i].y - p[i + 1].y));
        }
        s = abs(s);
        ll in = s / 2 - on / 2 + 1;
        printf("Case %d: ", _);
        printf("%lld\n", in);
    }
    return 0;
}