2019 杭电多校 第四场

2019 Multi-University Training Contest 4

补题链接：2019 Multi-University Training Contest 4

1001 AND Minimum Spanning Tree (HDU 6614)

题意

给定一个有 $N$ 个结点的完全图，编号从 $1$ 到 $N$。结点 $x$ 与结点 $y$ $(1\leq x, y\leq N, x \neq y)$ 的边的权值为 $x$ 与 $y$ 按位与的值，求该图的最小生成树。

题解

位运算

偶数与 1 按位与的值一定是 0，奇数与 1 按位与的值一定是 1。
因此，让所有的偶数结点与结点 $1$ 相连即可。
接着连接奇数结点。一个数 $x$ 与奇数按位与的值为 0，那么奇数二进制表示下中的 1 全部要变成 0。由于结点编号从 $1$ 到 $N$，那么结点不能取 $0$，因此 $x$ 二进制中至少包含一个 1。为了让 $x$ 尽可能的小（输出为字典序最小），可以让奇数二进制表示下的从右到左第一个 0 变成 1，如下表所示。

奇数	二进制	$x$
3	0011	0100
5	0101	0010
7	0111	1000
9	1001	0010
11	1011	0100
13	1101	0010
15	1111	10000

注意：如果奇数选择的最小结点大于 $N$，那么让该奇数结点与结点 $1$ 相连，边的权值为 1。
因此，偶数结点的边权一定为 0，奇数结点如果与偶数结点相连边权为 0，与结点 $1$ 相连权值为 1，保证总的边权最小，满足最小生成树。

#include <bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + 10;

int ans[maxn];

int main() {
    int T;
    cin >> T;
    while(T--) {
        int n;
        scanf("%d", &n);
        int cnt = 0;
        for(int i = 2; i <= n; ++i) {
            if(i % 2) {
                int tmp = i;
                int s = 0;
                while(tmp & 1) {
                    s++;
                    tmp >>= 1;
                }
                int t = 1 << s;
                if(t > n) {
                    ans[i] = 1;
                    cnt += 1;
                } else {
                    ans[i] = t;
                }
            } else {
                ans[i] = 1;
            }
        }
        printf("%d\n", cnt);
        for(int i = 2; i <= n; ++i) {
            printf("%d", ans[i]);
            printf("%s", i == n? "\n": " ");
        }
    }
    return 0;
}

1003 Divide the Stones (HDU 6616)

题意

给定两个整数 $n$ 和 $k$，将 $1 \sim n$ 的整数分成 $k$ 组，要求每组中的所有数的和相同且每组的数的个数也相同，求可行解。

题解

思维

分类讨论。

1. 当 $n$ 为偶数时，$n / k$ 也必须是偶数。然后蛇形取法即可。

2. 当 $n$ 为奇数时，$n / k$ 也必须是奇数。$k = 1$ 时特判。其余情况每组先分 $3$ 个，剩下的按照第一步的方法即可。

1007 Just an Old Puzzle (HDU 6620)

$solved by ch$

题意

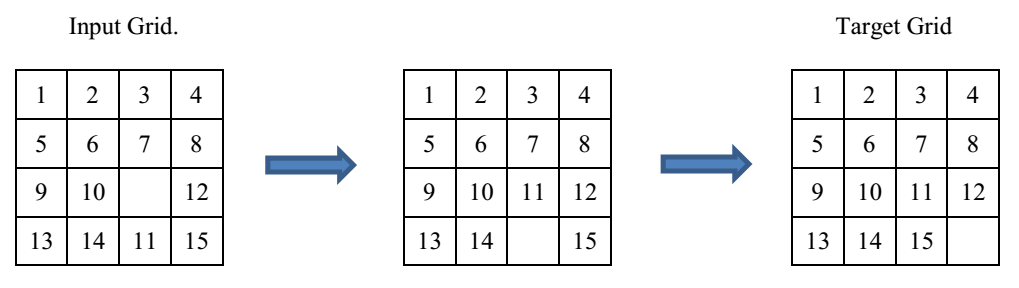
给定 $4 * 4$ 的方格，包含 $1$ 到 $15$ 的数和一个空格。空格可以和上下左右的数字块交换。试求是否能够在 $120$ 步移动空格使得方格变成图中的目标状态。

题解

逆序数

题目只需考虑是否有解，不需求出移动步数。即判断十五数码问题是否有解。
满足下列条件一定有解。

1. 若格子列数为奇数，则逆序数必须为偶数；
2. 若格子列数为偶数，且逆序数为偶数，则当前空格所在行数与初始空格所在行数的差为偶数；
3. 若格子列数为偶数，且逆序数为奇数，则当前空格所在行数与初始空格所在行数的差为奇数。

参考

数字华容道怎样才能有解

#include <bits/stdc++.h>
using namespace std;
int a[17];
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int cnt=0,it;
        for(int i=1;i<=16;i++)
        {
            scanf("%d",&a[i]);
            if(a[i]==0)
            {
                if(i%4==0) it=i/4;
                else it=1+i/4;
            }
        }
        for(int i=2;i<=16;i++)
        {
            if(a[i]==0) continue;
            for(int j=1;j<i;j++)
            {
                if(a[j]>a[i])
                    cnt++;
            }
        }
        //cout<<cnt<<" "<<it<<endl;
        if(cnt%2==0)
        {
            if(abs(4-it)%2==0) printf("Yes\n");
            else printf("No\n");
        }
        else
        {
            if(abs(4-it)%2==0) printf("No\n");
            else printf("Yes\n");
        }
    }
    return 0;
}

1008 K-th Closest Distance (HDU 6621)

$solved by ch$

题意

给定一个 $a_1 … a_n$ 的数组。给定 $m$ 个询问，每个询问包含四个整数 $L$， $R$， $p$， $K$，求 $\{|a_L - p|, |a_{L+1} - p|, … ,|a_R -
p|\}$ 中第 $K$ 大的数。

题解

二分 排序 离散化

记录所有数的下标，对所有数离散化，查找 $p$ 的位置，往左往右分别找 $k$ 个数，使得这些数的下标在区间 $[L, R]$ 内，对所有找到的数排序，第 $k$ 大的数即是答案。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef struct DATE
{
    int id, val;
} D;
D date[100010];
bool cmp1(D a, D b)
{
    return a.val < b.val;
}
vector<int> id[100010];
int a[100010];
int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        memset(a, 0, sizeof(a));
        int n, m, num = 0, Xor = 0;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
        {
            date[i].id = i;
            scanf("%d", &date[i].val);
        }
        sort(date + 1, date + n + 1, cmp1);
        for (int i = 1; i <= n; i++)
        {
            if (a[num] != date[i].val)
                a[++num] = date[i].val;
            id[num].push_back(date[i].id);
        }
        for (int i = 1; i <= num; i++)
        {
            sort(id[i].begin(), id[i].end());
        }
        for (int i = 0; i < m; i++)
        {
            int l, r, L, R, it, p, k, x[1010], tmp = 0;
            scanf("%d%d%d%d", &l, &r, &p, &k);
            l ^= Xor, r ^= Xor, k ^= Xor, p ^= Xor;
            it = lower_bound(a + 1, a + num + 1, p) - a;
            int tmp1 = 0, tmp2 = 0;
            for (int j = it - 1; j >= 1 && tmp1 <= k; j--)
            {
                L = lower_bound(id[j].begin(), id[j].end(), l) - id[j].begin();
                while (L < id[j].size() && id[j][L] <= r)
                {
                    x[tmp++] = abs(a[j] - p);
                    L++;
                    tmp1++;
                    if (tmp1 > k)
                        break;
                }
            }
            for (int j = it; j <= num && tmp2 <= k; j++)
            {
                L = lower_bound(id[j].begin(), id[j].end(), l) - id[j].begin();
                while (L < id[j].size() && id[j][L] <= r)
                {
                    x[tmp++] = abs(a[j] - p);
                    L++;
                    tmp2++;
                    if (tmp2 > k)
                        break;
                }
            }
            sort(x, x + tmp);
            Xor = x[k - 1];
            printf("%d\n", x[k - 1]);
        }
        for (int i = 1; i <= num; i++)
            id[i].clear();
    }
    return 0;
}

1010 Minimal Power of Prime (HDU 6623)

题意

给定一个整数 $n > 1$，分解质因数后，求最小的指数。

题解

素数筛 质因数分解

由于 $3982^4 > 10^{18}$，那么所有大于 $3982$ 的数的指数最多为 $4$。
先筛出 $4000$ 以内的所有质数，将 $n$ 暴力分解质因数。如果 $n$ 还没分解完，那么剩下的数分解质因数后的指数只能是 $1$ 到 $4$ 之间，从大到小枚举即可。

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

ll n;
int ans;

vector<int> primes;
int is_prime[4000];

void sieve() {
    is_prime[0] = is_prime[1] = 1;
    for(int i = 2; i < 4000; ++i) {
        if(!is_prime[i]) {
            primes.push_back(i);
        }
        for(int j = 0; j < primes.size() && i * primes[j] < 4000; ++j) {
            is_prime[i * primes[j]] = 1;
            if(i % primes[j] == 0) break;
        }
    }
}

void solve() {
    for(int i = 0; i < primes.size() && primes[i] * primes[i] <= n; ++i) {
        int cnt = 0;
        if(n % primes[i] == 0) {
            while(n % primes[i] == 0) {
                cnt++;
                n /= primes[i];
            }
            ans = min(ans, cnt);
        }
    }
    if(n == 1 || ans == 1) {
        printf("%d\n", ans);
        return;
    }
    int flag = 0;
    for(int i = 4; i >= 2; --i) {
        ll num = pow(n, 1.0 / i);
        for(ll j = num - 3; j < num + 3; ++j) {
            ll res = 1;
            for(int k = 0; k < i; ++k) res *= j;
            if(res == n) {
                flag = 1;
                break;
            }
        }
        if(flag) {
            ans = min(ans, i);
            break;
        }
    }
    if(flag) {
        printf("%d\n", ans);
    } else {
        printf("1\n");
    }
}

int main() {
    sieve();
    // for(int i = 0; i < 30; ++i) cout << primes[i] << endl;
    int T;
    scanf("%d", &T);
    while(T--) {
        ans = 65;
        scanf("%lld", &n);
        solve();
        // printf("%d\n", ans);
    }
    return 0;
}