WuTao's Blog

while(!(succeed = try()));

0%

2019 杭电多校 第十场

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 5.5k 阅读时长 ≈ 5 分钟

2019 Multi-University Training Contest 10

补题链接：2019 Multi-University Training Contest 10

1003 Valentine’s Day (HDU 6693)

题意

有 $n$ 种礼物，第 $i$ 种礼物能让女朋友开心的概率为 $P_i$，挑一些礼物，问让女朋友开心一次的概率最大为多少。

题解

概率 贪心

如果有概率大于等于 $0.5$ 的礼物，输出其中最大的。

否则，对概率从大到小。暴力枚举选择前 $k$ 大的礼物的的概率，求最大值即可。

此题有原题。见 CodeForces 442B

相关证明见官方题解：Codeforces #253 editorial

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double eps = 1e-8;
const int inf = 0x3f3f3f3f;
const int maxn = 100000 + 5;

double p[maxn];

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        int n;
        scanf("%d", &n);
        double ans = 0, maxa = -1;
        int flag = 0;
        for(int i = 0; i < n; ++i) {
            scanf("%lf", &p[i]);
            if(p[i] >= 0.5) {
                flag = 1;
                if(maxa = -1) maxa = p[i];
                else maxa = max(maxa, p[i]);
            }
        }
        if(flag) {
            printf("%.6lf\n", maxa);
        } else {
            sort(p, p + n);
            double tmp1 = p[n - 1];
            double tmp2 = p[n - 1] * (1 - p[n - 2]) + p[n - 2] * (1 - p[n - 1]);
            ans = tmp2;
            int k = 3;
            while(tmp1 < tmp2 && k <= n) {
                ans = tmp2;
                tmp1 = tmp2;
                tmp2 = 0;
                for(int i = n - 1; i >= n - k; --i) {
                    double tmp = 1;
                    for(int j = n - 1; j >= n - k; --j) {
                        if(j == i) {
                            tmp *= p[j];
                        } else {
                            tmp *= 1 - p[j];
                        }
                    }
                    tmp2 += tmp;
                }
                k ++;
            }
            printf("%.6lf\n", max(ans, tmp2));
        }
    }
    return 0;
}

1005 Welcome Party (HDU 6695)

$solved by ch$

题意

有 $n$ 个人，$2$ 种节目，每个人要表演其中的一种节目，每种节目至少有一人表演。用 $x_i$ 和 $y_i$ 表示第 $i (1\le i\le n)$ 个人表演两种节目的能力值。现在要使表演第一种节目的人中的能力最大值与表演第二种节目的人中的能力最大值之差最小，求这个最小值。

题解

贪心

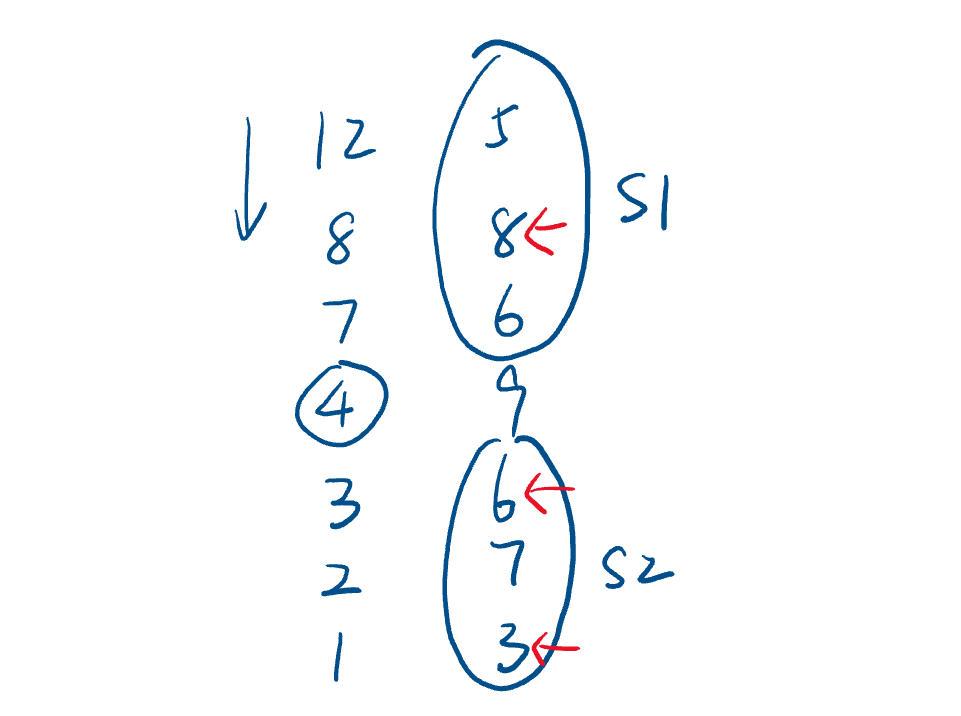
如下图，维护两个集合 $s_1$ 和 $s_2$。

按 $x$ 从大到小枚举。假设 $x_i$ 为 $x$ 中的最大值 (下图中的 $4$)，则比 $x_i$ 大的都选择 $y$，也就是取 $s_1$ 中的最大值 (下图中的 $8$)。比 $x_i$ 小的取与 $x_i$ 最接近的 $y$ (下图中的 $3$)，因为更大的 $y$ 可以选择 $x$ (下图中的 $7$ 可以用 $2$ 替换)。然后取两个的较大值更新到 $ans$ (下图中 $|3 - 4| < |8 - 4|$ 取 $8 - 4$)，维护最小值 $ans$ 即可。

比赛中队友 (线段树大佬) 用线段树过的。赛后我用 $multiset$ 写了一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const ll inf = 2e18;

struct STU {
    ll x, y;
} s[maxn];
ll maxy[maxn];

int cmp(STU s1, STU s2) {
    return s1.x > s2.x;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--) {
        int n;
        cin >> n;
        multiset<ll> s1, s2;
        for(int i = 0; i < n; ++i) {
            cin >> s[i].x >> s[i].y;
            s2.insert(s[i].y);
        }
        sort(s, s + n, cmp);
        ll ans = inf;
        for(int i = 0; i < n; ++i) {
            s2.erase(s2.find(s[i].y));  // 一个人只能选择一种表演
            if(!s1.empty()) {
                ans = min(ans, abs(*s1.rbegin() - s[i].x));
            }
            if(!s2.empty()) {
                multiset<ll>::iterator it = s2.lower_bound(s[i].x); // 找到第一个大于等于 s[i].x 的 y
                if(it == s2.end()) {
                    --it;
                }
                ll tmp = abs(*it - s[i].x);
                if(tmp < ans && (s1.empty() || *it > *s1.rbegin())) {
                    ans = tmp;
                }
                if(it != s2.begin()) {  // 找到最后一个小于 s[i].x 的 y
                    --it;
                    tmp = abs(*it - s[i].x);
                    if(tmp < ans && (s1.empty() || *it > *s1.rbegin())) {
                        ans = tmp;
                    }
                }
                s1.insert(s[i].y);
            }
        }
        cout << ans << endl;
    }
    return 0;
}

1007 Closest Pair of Segments (HDU 6697)

题意

类似于计算几何中的最近点对问题，本题求的是最近线段对。

给定 $n$ 条线段，求出最近线段对之间的距离。

题解

暴力 剪枝

比赛时我用了三角剖分，结果超时了。

赛后补题时看到了这篇博客：HDU 6697 Closest Pair of Segments（线段距离）

原来暴力加上剪枝就能过。思路是这样的：

首先将线段的左侧端点按照横坐标为第一关键字，纵坐标为第二关键字排序。然后暴力找所有线段对，维护最小值 $ans$。如果当前查询的线段对中，右侧线段的左端点与左侧线段的右端点的横坐标差值大于 $ans$ 时，就不用再找更右侧的直线了。这样剪枝能大大减少时间复杂度。

时限给了 20s，大概 1.3s 就能跑完。

题解看不懂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

struct Point {
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
    }
    bool operator==(const Point &a) const {
        return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
    }
    db dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }

    db dis(const Point a) {
        return sqrt(dis2(a));
    }

    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }

};
typedef Point Vector;

struct Line {
    Point s, e;
    Line() {}
    Line(Point s, Point e) : s(s), e(e) {}
    void input() {
        s.input();
        e.input();
    }
    db length() {
        return s.dis(e);
    }

    // 点到直线的距离
    db point_to_line(Point p) {
        return fabs((p - s).cross(e - s) / length());
    }

    // 点到线段的距离
    db point_to_seg(Point p) {
		if(dcmp((p - s).dot((e - s))) < 0 || dcmp((p - e).dot((s - e))) < 0) {
			return min(p.dis(s), p.dis(e));
		}
		return point_to_line(p);
    }

    // 线段到线段的距离
    db seg_to_seg(Line l) {
		return min(min(point_to_seg(l.s), point_to_seg(l.e)), min(l.point_to_seg(s), l.point_to_seg(e)));
    }
};

Line l[maxn];

int cmp(Line l1, Line l2) {
	return l1.s < l2.s;
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        int n;
        scanf("%d", &n);
        for(int i = 0; i < n; ++i) {
            l[i].input();
			if(l[i].e < l[i].s) swap(l[i].s, l[i].e);
        }
		sort(l, l + n, cmp);
		double ans = 1e10;
		for(int i = 0; i < n; ++i) {
			for(int j = i + 1; j < n; ++j) {
                // 剪枝部分
				if(dcmp((l[j].s.x - l[i].e.x) - ans) > 0) {
					break;
				}
				ans = min(ans, l[i].seg_to_seg(l[j])); // 更新最小值
			}
		}
		printf("%.12lf\n", ans);
    }
    return 0;
}

1009 Block Breaker (HDU 6699)

$solved by zmz$

队友签的到。

欢迎关注我的其它发布渠道