HDU 6695 Welcome Party (贪心)

2019 杭电多校 10 1005

题目链接：HDU 6695

比赛链接：2019 Multi-University Training Contest 10

Problem Description

The annual welcome party of the Department of Computer Science and Technology is coming soon! Many students have been applying to show up at the welcome party, and every one of them can choose to sing a song or play crosstalk. This troubles the chief director a lot: how to arrange the program list, such that every student can have a chance to show up on the stage, and the satisfactory value of audiences is maximized?

To cope with this problem, the director proposes a model. In this model, every student has two attributes: the singing ability and crosstalking ability. The satisfactory value of audiences to singings is the maximum singing ability among all students that choose to sing a song; similarly, the satisfactory value to crosstalks is the maximum crosstalking ability among all students that choose play crosstalk. The strange thing is, the overall satisfactory value to the whole party is negatively related to the absolute difference between the satisfactory values to singings and crosstalks. The problem is, what is the minimum possible absolute difference between the satisfactory values of the two types of programs?

Note that:

• every student should choose exactly one type of programs to play;
• at least one student should sing a song, and at least one student should play crosstalk.

Input

The first line of input consists of a single integer $T (1\le T\le 70)$, the number of test cases.

Each test case starts with a line of a single integer $n (2\le n\le 100000)$, denoting the number of students applying to show up on the stage. Then follow $n$ lines, each containing two integers $x$ and $y (0\le x,y\le 10^{18})$, denoting the singing ability and crosstalking ability of a student.

It is guaranteed that the sum of $n$ over all test cases never exceeds $1000000$.

Output

For each test case, output a single integer, denoting the minimum possible absolute difference between the satisfactory values of the two types of programs.

Sample Input

2
5
27 46
89 13
55 8
71 86
22 35
3
3 5
4 7
6 2

Sample Output

3
1

Solution

题意

有 $n$ 个人，$2$ 种节目，每个人要表演其中的一种节目，每种节目至少有一人表演。用 $x_i$ 和 $y_i$ 表示第 $i (1\le i\le n)$ 个人表演两种节目的能力值。现在要使表演第一种节目的人中的能力最大值与表演第二种节目的人中的能力最大值之差最小，求这个最小值。

题解

贪心

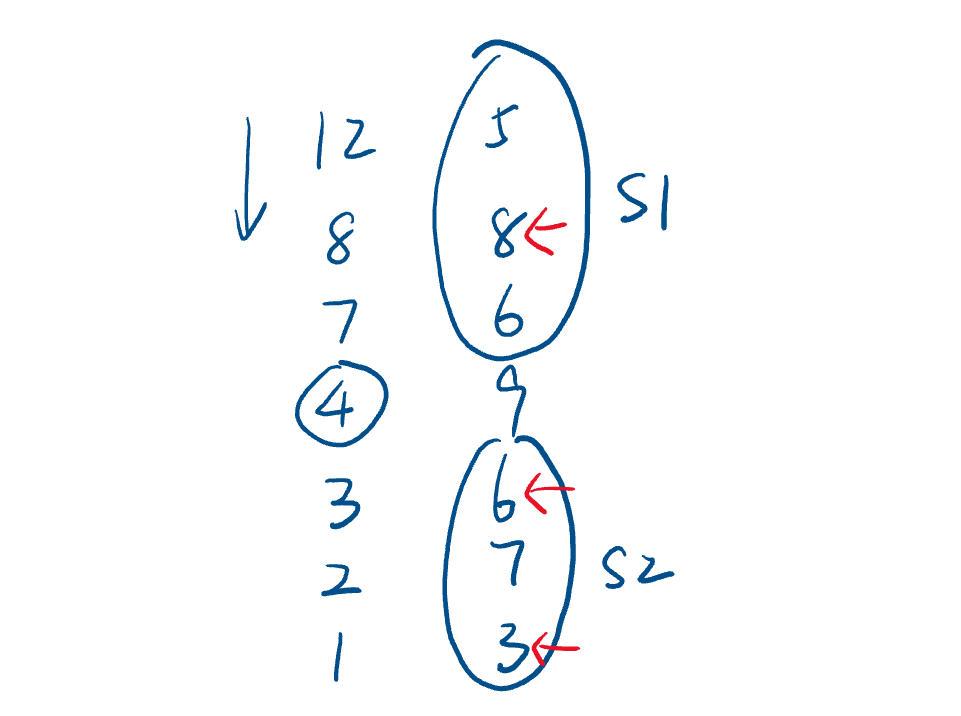
如下图，维护两个集合 $s_1$ 和 $s_2$。

按 $x$ 从大到小枚举。假设 $x_i$ 为 $x$ 中的最大值 (下图中的 $4$)，则比 $x_i$ 大的都选择 $y$，也就是取 $s_1$ 中的最大值 (下图中的 $8$)。比 $x_i$ 小的取与 $x_i$ 最接近的 $y$ (下图中的 $3$)，因为更大的 $y$ 可以选择 $x$ (下图中的 $7$ 可以用 $2$ 替换)。然后取两个的较大值更新到 $ans$ (下图中 $|3 - 4| < |8 - 4|$ 取 $8 - 4$)，维护最小值 $ans$ 即可。

比赛中队友 (线段树大佬) 用线段树过的。赛后我用 $multiset$ 写了一下。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const ll inf = 2e18;

struct STU {
    ll x, y;
} s[maxn];
ll maxy[maxn];

int cmp(STU s1, STU s2) {
    return s1.x > s2.x;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin >> T;
    while(T--) {
        int n;
        cin >> n;
        multiset<ll> s1, s2;
        for(int i = 0; i < n; ++i) {
            cin >> s[i].x >> s[i].y;
            s2.insert(s[i].y);
        }
        sort(s, s + n, cmp);
        ll ans = inf;
        for(int i = 0; i < n; ++i) {
            s2.erase(s2.find(s[i].y));  // 一个人只能选择一种表演
            if(!s1.empty()) {
                ans = min(ans, abs(*s1.rbegin() - s[i].x));
            }
            if(!s2.empty()) {
                multiset<ll>::iterator it = s2.lower_bound(s[i].x); // 找到第一个大于等于 s[i].x 的 y
                if(it == s2.end()) {
                    --it;
                }
                ll tmp = abs(*it - s[i].x);
                if(tmp < ans && (s1.empty() || *it > *s1.rbegin())) {
                    ans = tmp;
                }
                if(it != s2.begin()) {  // 找到最后一个小于 s[i].x 的 y
                    --it;
                    tmp = abs(*it - s[i].x);
                    if(tmp < ans && (s1.empty() || *it > *s1.rbegin())) {
                        ans = tmp;
                    }
                }
                s1.insert(s[i].y);
            }
        }
        cout << ans << endl;
    }
    return 0;
}